本系列是C/C++描述编写。
绪论
程序设计=数据结构+算法(Algorithm+Data Structures=Programs)是瑞士计算机科学家尼古拉斯·沃斯在1984年获得图灵奖的一句话。
什么是数据结构
数据结构(data structure)是一门研究非数值计算的程序设计问题中的操作对象,以及它们之间的关系和操作等问题的学科。
数据结构是计算机存储、组织数据的方式,也就是数据元素互相存在的一种或多种特定关系的集合。
传统上,我们将数据结构分为逻辑结构(指数据对象中数据元素间的互相关系)和物理结构(指数据的逻辑结构在计算机中的存储方式)。
四大逻辑结构
集合结构
指具有某种特定性质的数据元素汇总而成的集体。
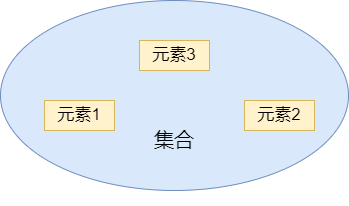
线性结构
指数据元素间是一对一的关系。

树形结构
指数据元素之间存在一种一对多的层级关系。
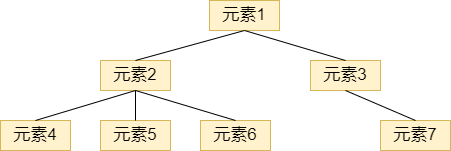
图形结构
指数据元素间是多对多的关系。

物理结构
实际上就是如何将数据元素存储到计算机的存储器(主要是对内存而言的,像硬盘、软盘、光盘等外部存储器的数据组织通常用文件结构来买描述)中。
顺序存储
就是把数据元素存放在地址连续的存储单元里,其逻辑关系和物理关系一致,类似我们C语言中的数组。
链式存储
是把数据元素存放在任意的存储单元里,这组存储单元可以是连续的,也可以是不连续的。由此需要用一个指针来存放相关数据的地址。可以类比指针数组。
什么是算法
算法(algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。
算法和数据结构离不开彼此,可以说算法就是为了处理相应的数据结构并高效的解决问题。
就如求1+2+3+…+123456789的和:
在普通方法下,采用一个123456789次的循环累加,但这毫无疑问要花费大量时间和空间。
但如果使用等差数列求和的算法公式:首项加末项乘以项数除以2。只要一步就可以完成计算。
五个特征
一个典型的算法一般都可以抽象出5个特征:
-
有穷性:算法的指令或者步骤的执行次数和时间都是有限的。
-
输入:有相应的输入条件(可以没有输入)来刻画运算对象的初始情况。
-
输出:一个算应有明确的结果输出。
-
确切性:算法的指令或步骤都有明确的定义,相同输入有相同的输出。
-
可行性:算法的执行步骤必须是可行的。
复杂度
我们使用算法就是为了更高的效率,由此我们需要用某种简单高效的不受编程语言和测试环境影响的方法来衡量一个算法的好坏,这就有了算法的时间复杂度和空间复杂度。
时间复杂度
我们把基本操作也就是将一句语句抽象看为1。
就如C语言:
a += 1;这时间复杂度就是1。
for(int i=0 ; i<n ; i++) { a ++; }此例的时间复杂度为n。
for(int i=0 ; i<n ; i++) { for(int j=0 ; j<n ;j++) { a += j*i; } }此时的时间复杂度为n^2^。
int i = 1; int n = 100; whlie(i < n) { i *=2; }这个的时间复杂度为log~2~n。
衡量方法
| n | 4n+8 | n^2^ | 2n^2^+1 | n^3^ | |
|---|---|---|---|---|---|
| n=1 | 1 | 12 | 1 | 3 | 1 |
| n=2 | 2 | 16 | 4 | 9 | 8 |
| n=3 | 3 | 20 | 9 | 19 | 27 |
| n=10 | 10 | 48 | 100 | 201 | 1000 |
| n=100 | 100 | 408 | 10000 | 20001 | 1000000 |
| n=1000 | 1000 | 4008 | 1000000 | 2000001 | 10^9^ |
画出函数图,当n较小(0~10)时:
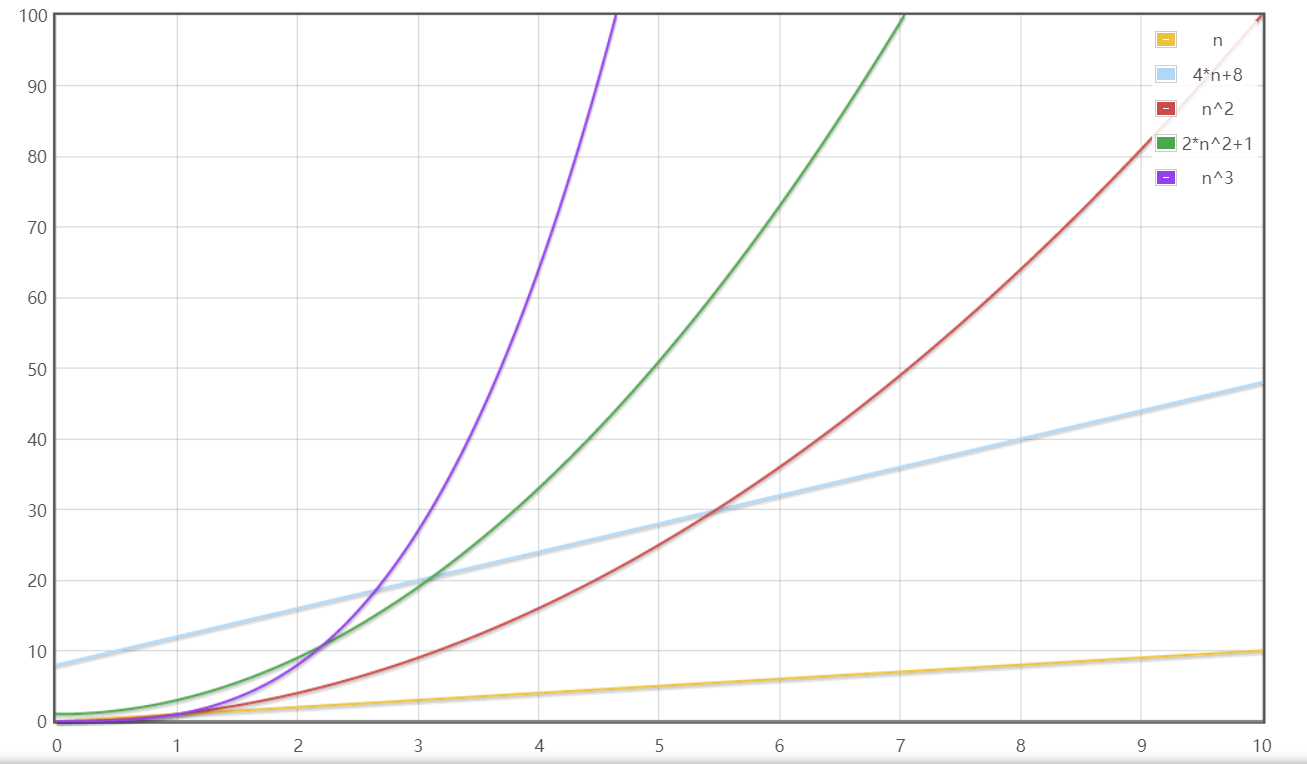
当n变大(0~100)时:
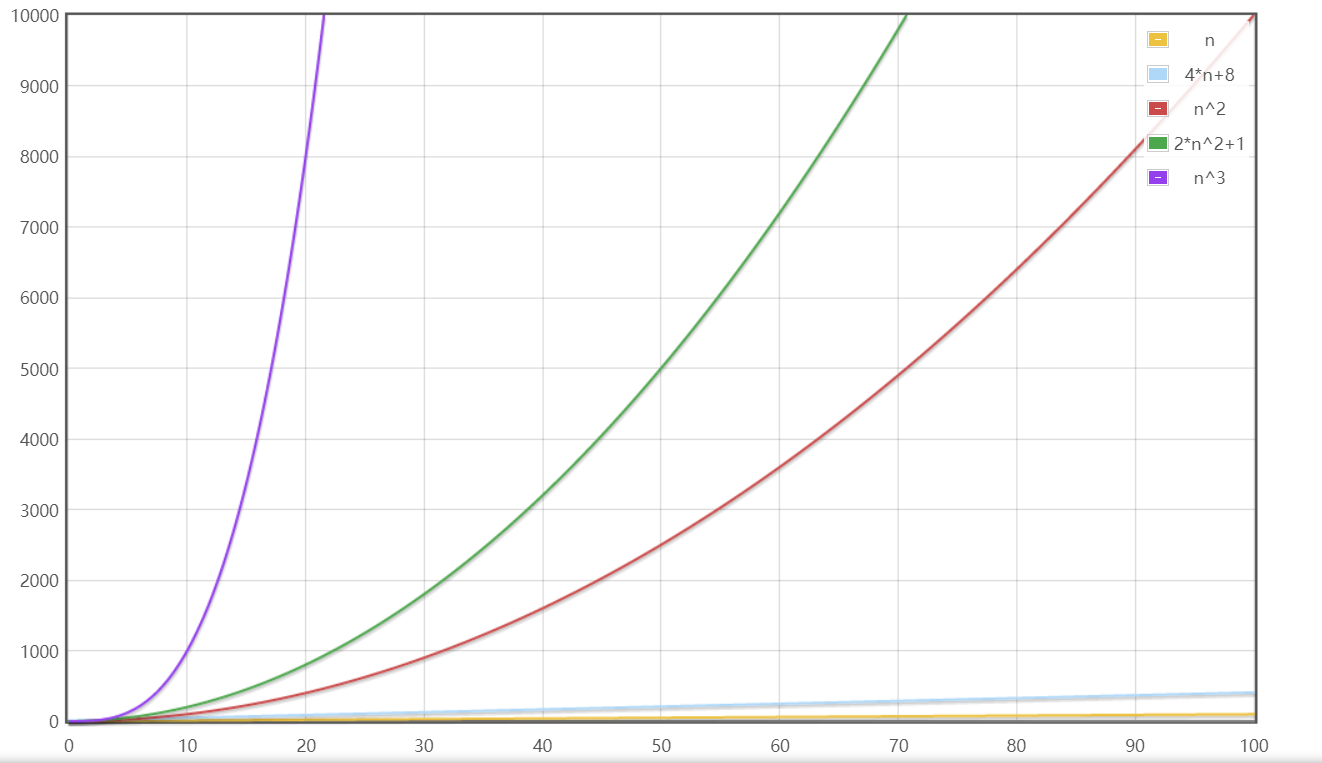
当n较大(0~1000)时:
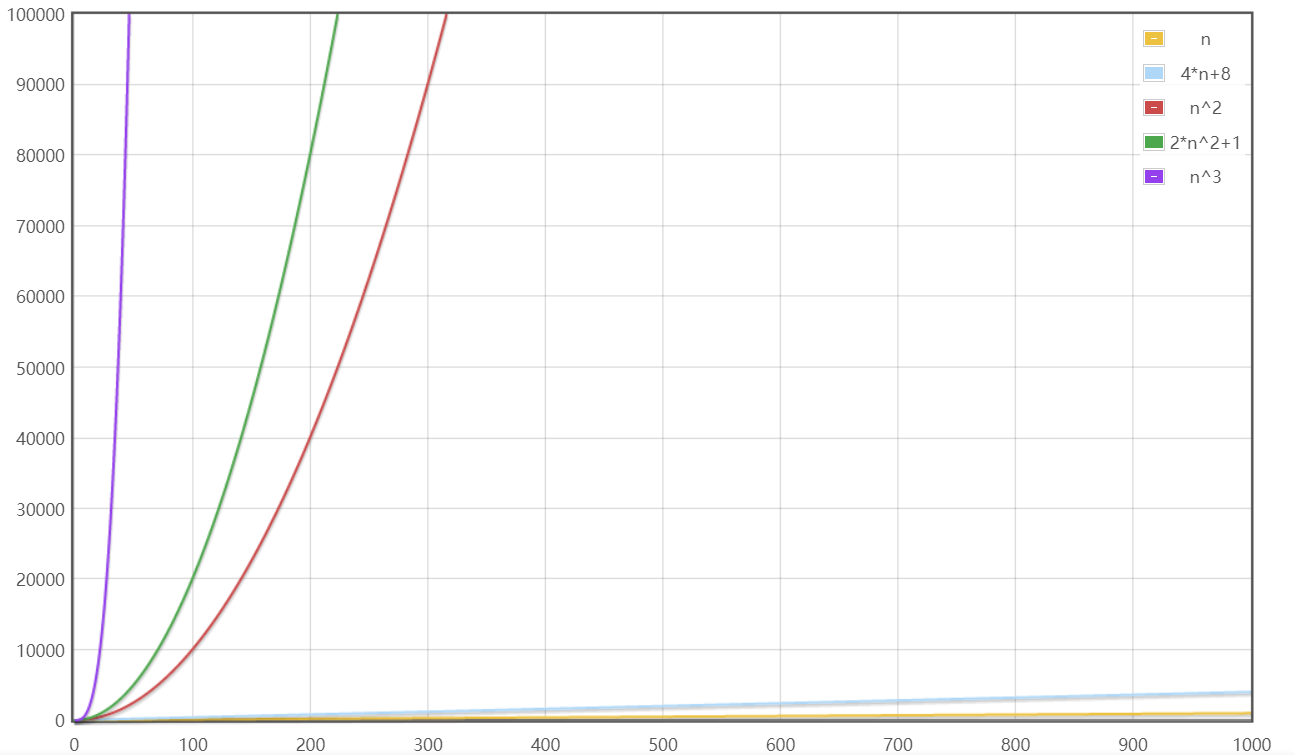
从表格和图中我们可以在n较小时看出各个算法时间复杂度参差不齐,但随着n变大增长速率大的算法时间复杂度变得越来越大,远远超过增长速率小的算法。
由此总结出了衡量时间复杂度的方法:考虑增长速率,同时当n取较大时可以忽略表达式的常数项和其他次要项,只保留最高项的阶数。公式就是T(n)=O(f(n))。
T(n)表示时间复杂度,f(n)表示算法的时间复杂度表达式,O(n)表示衡量方法。如:
f(n) T(n) 术语 3 O(1) 常数阶 n O(n) 线性阶 4n+8 O(n) 线性阶 n^2^ O(n^2^) 平方阶 2n^2^+1 O(n^2^) 平方阶 log~2~n O(log~2~n) / O(logn) 对数阶 nlog~2~n O(nlog~2~n) / O(nlogn) nlog~2~n阶 n^3^ O(n^3^) 立方阶 2^n^ O(2^n^) 指数阶 耗时从小到大:O(1) < O(log~2~n) < O(n) < O(nlog~2~n) < O(n^2^) < O(n^3^) < O(2^n^) < O(n!) < O(n^n^)
在一般情况下我们看一个算法会计算其最好的时间复杂度和最坏的,并求出平均时间复杂度(最坏的减去最好的,然后除以2),以此衡量。
空间复杂度
是对算法运行过程中临时占用空间大小的度量,公式和时间复杂度类似:S(n) = O(f(n)) ,其中 n 为问题的规模, S(n) 表示空间复杂度。
int a = 1; int b = 2; a = a + b;此时S(n)=O(1)。
int b = 0; for (int i=0 ; i<n ; i++) { int a = i; b += a; }此例的S(n)=O(n)。
int b[n]; for (int i=0 ; i<n ; i++) { b[i] = i; }此例的S(n)也是O(n)。
常见的空间复杂度不多,从低到高排列有: O(1) < O(log~2~(n)) < O(n) < O(n^2^)
时间和空间的关系
对于一个算法来说,它的时间复杂度和空间复杂度往往是相互影响的。
当追求一个较好的时间复杂度时,可能需要消耗更多的储存空间。反之,如果追求较好的空间复杂度,算法执行的时间可能就会变长。
我们通常用空间换时间。就拿Chrome来说,其流畅性高,但是也占用较大的内存空间。
抽象数据类型
抽象是指抽取出事物具有的普遍性的本质,是对一类具体事物的概括。
数据类型是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。如整形、浮点型、字符型。
我们将常用的数据类型抽象就有了抽象数据类型(Abstract Data Type,ADT),并给出了抽象数据类型的标准形式:
ADT 抽象数据类型名
Data
数据元素之间逻辑关系的定义
Operation
操作
endADT本系列都有参考:










