链表

上篇中讲到顺序存储结构的线性表不适合大量的插入和删除，而链式存储结构的线性表（链表 linked list）刚好可以解决这个问题。

链表的特点是：用一组任意的存储单元存储线性表的数据元素，也就是说这些存储单元在内存中未被占用的任意位置。

为了实现上面的特点，在链表中除了要存储数据还要存放后继（或前驱）元素的地址。我们把存储数据元素信息的域称为数据域，把存储元素地址的域称为指针域。这两部分组成的数据元素称为存储映像，也就是链表的结点（Node）。

链表从指针域来划分有：单链表、双链表、单向循环链表、双向循环链表。

链表从存储来划分有：静态链表、动态链表。动态链表是指动态的管理结点，而静态链表是指用数组描述的链表（这在后面会展开）。

单链表

结点中的只有一个指针域，且指向其直接后继元素的链表叫单链表，单链表的最后一个结点的指针域为空。我们把链表的第一个结点叫头结点，且通常不放数据，头指针总是指向头结点。

下面是动态单链表示意图：

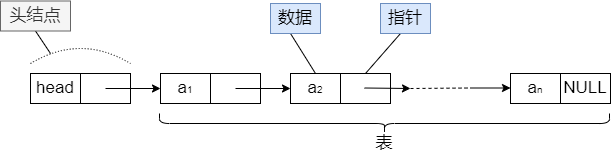
空单链表图：

实现

构建结点

typedef int Elem_Type;
/* C语言要加这些，C++不用 */
typedef struct Node Node;
typedef int bool;
#define true 1
#define false 0

struct Node // 结点
{
    Elem_Type data; // 数据域
    Node * next_Node; // 指针域
} *head; // 声明头指针
typedef struct Node Linked_List; // 方便区分代码中使用链表

初始化

由于这里采用的头指针在堆上，所以如果要在函数里改变头指针的指向就要用到二级指针。

初始化完成后就有了一个空的单链表。

void init_list(Linked_List **head) // 将头指针改变指向头节点，因此参数是指针的指针
{
    *head = (Node *)malloc(sizeof(Node)); // 申请头节点空间
    (*head)->data = 0; // 头节点数据域初始化但不放数据
    (*head)->next_Node = NULL; // 建立空表，C++中可以把NULL全替换为nullptr
}

清空

由于我们采用的是动态单链表，所以对于动态链表的清空都要一个一个结点释放。

同时由于我们并没有定义存储表长的变量，所以不知道要循环多少次，因此不方便用for循环，而是用while通过工作指针后移来实现。

清楚完毕后为空表，因此头节点不要释放。

void clear_list(Linked_List *head)
{
    Node *temp = NULL; // 临时存放要释放的下一个结点
    Node *free_node = head->next_Node; // 存放要释放的结点
    /* 遍历清除 */
    while(free_node != NULL)
    {
        temp = free_node->next_Node; // 存放要释放的下一个结点
        free(free_node); // 释放结点
        free_node = temp; // 准备释放下一个节点
    }
    head->next_Node = NULL;
}

判空

bool list_is_empty(Linked_List head)
{
    if(head.next_Node == NULL) // 是否空表
    {
        return true;
    }
    return false;
}

获取表长

遍历一般链表就能知道表长。

int list_length(Linked_List head)
{
    int count = 0; // 统计长度
    Node *temp = head.next_Node; // 临时存放每一个结点
    /* 遍历计数 */
    while(temp != NULL)
    {
        count++;
        temp = temp->next_Node;
    }
    return count;
}

按值查找

按值查找是采用遍历的方式，因此时间复杂度也是O(n)，和顺序存储结构的线性表一样。

int list_locate_elem(Linked_List head,Elem_Type e)
{
    int count = 0; // 存放元素在表中的位置
    Node *temp = head.next_Node; // 临时存放遍历结点
    /* 遍历定位 */
    while(temp != NULL)
    {
        count++;
        if(temp->data == e) // 找到元素
        {
            return count;
        }
        temp = temp->next_Node;
    }
    return 0;
}

按位查找并获取

单链表的按位查找也要遍历，因此时间复杂度同样为O(n)，因此链表不能随机访问，同时查找效率也比不过顺序存储结构。

bool list_get_elem(Linked_List head,int i,Elem_Type *e)
{
    Node *temp = head.next_Node; // 临时存放遍历结点
    int count = 1; //  计数，到i时停止查找
    /* 定位遍历 */
    while(temp!=NULL && count<i )
    {
        temp = temp->next_Node;
        count++;
    }
    /* 定位失败 */
    if(temp==NULL || count>i) // 没找到元素或传入的i<1
    {
        return false;
    }

    *e = temp->data;
    return true;
}

插入

插入的思路主要为三步：

找到要插入的位置；
当i<1或i超出可插入范围（i>表长+1）时，返回插入失败；
找到指定位置后，申请插入结点的空间，最后插入。

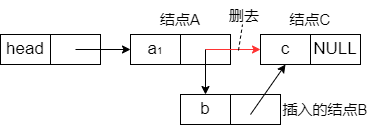
下图是插入的操作，可以总结为两句伪代码：B->Next_Node = A->NextNode; A->Next_Node = B;。

bool list_insert(Linked_List *head,int i,Elem_Type e)
{
    Node *temp = head; // 找出要插入的前一个结点
    Node *insert_node = NULL; // 要插入的结点
    int count = 1; // 计数
    /* 遍历到要插入的前一个结点 */
    while(count<i && temp!=NULL)
    {
        temp = temp->next_Node;
        count++;
    }
    /* 插入失败 */
    if(count>i || temp==NULL) // i<1或i超出可插入范围（i>表长+1）
    {
        return false;
    }

    insert_node = (Node *)malloc(sizeof(Node)); // 申请插入的结点空间
    insert_node->data = e;
    /* 插入 */
    insert_node->next_Node = temp->next_Node;
    temp->next_Node = insert_node;
    return true;
}

删除

删除的思路和插入类似也是三步：

找到要删除的位置；
当i<1或i超出可插入范围（i>表长+1）时，返回删除失败；
找到指定位置后进行删除操作。

下图是删除的核心操作，可以总结为两句伪代码：A->Next_Node = B->Next_Node; free(B);。

bool list_delete(Linked_List *head,int i,Elem_Type *e)
{
    Node *temp = head; // 存放要删除的前一个结点
    Node *deleted_node = NULL; // 要删除的结点
    int count = 1;
    /* 找出要删除的前一个结点 */
    while(temp!=NULL && count<i)
    {
        temp = temp->next_Node;
        count++;
    }
    /* 删除失败 */
    if(count>i || temp==NULL) // i<1或i超出可插入范围（i>表长+1）
    {
        return false;
    }
    /*删除*/
    deleted_node = temp->next_Node;
    temp->next_Node = deleted_node->next_Node;
    *e = deleted_node->data; // 取出删除的数据
    free(deleted_node);
    return true;
}

从上面的两断代码可以看出链表的插入和删除单个元素的时间复杂度也是O(n)，这和顺序结构的比起来似乎也没有什么优势。

但当一次插入或删除多个元素时，顺序结构的只能重复多次O(n)的操作，而链表却可以通过将第一次插入或删除的指针记下，此后的插入或删除都只要O(1)了。

头插法

头插法是插入的一种特例，即一直在头节点后插入数据。

/* 方法一 */
void list_push_front(Linked_List *head,Elem_Type e)
{
    Node *temp = NULL; // 要插入的结点
    temp = (Node *)malloc(sizeof(Node));
    temp->data = e;
    /* 插入 */
    temp->next_Node = head->next_Node;
    head->next_Node = temp;
}

/* 方法二 */
void list_push_front(Linked_List *head,Elem_Type e)
{
    list_insert(head,1,e);
}

尾插法

头插法也是插入的一种特例，顾名思义就是一直在链表尾部插入数据。

void list_push_back(Linked_List *head,Elem_Type e)
{
    Node *temp = head; // 最后的结点
    /* 遍历到最后的结点 */
    while(temp->next_Node != NULL)
    {
        temp = temp->next_Node;
    }
    /* 插入新节点 */
    temp->next_Node = (Node *)malloc(sizeof(Node));
    temp->next_Node->data = e;
    temp->next_Node->next_Node = NULL;
}

其他部分

void create_10elem_list(Linked_List *head)
{
    for(int i=1 ; i<=10 ; i++)
    {
        list_push_back(head,i); // 尾插法插入10个元素
    }
}

void print_list(Linked_List head) // 打印链表
{
    Node *temp = head.next_Node;
    while(temp != NULL)
    {
        if(sizeof(Elem_Type) == 4) // 若Elem_Type是int时
        {
            printf("%d ",temp->data);
        }
        temp = temp->next_Node;
    }
    printf("\n");
}

算法小题

题目：快速找到未知长度单链表的中间元素。

思路：

普通方法：遍历数组找出长度L，然后再次从头出发循环L/2次找到中间元素。时间复杂度：O(3L/2)
快慢指针（标尺）：设置两个指针fast和slow，fast指针的移动速度是slow的两倍,当fast到链表结尾时slow刚好在中间结点。时间复杂度：O(L/2)

实现代码：

bool get_mid_elem(Linked_List *head,Elem_Type *e)
{
    Node *fast = head; // 快指针
    Node *slow = head; // 慢指针
    while(fast->next_Node != NULL)
    {
        if(fast->next_Node->next_Node != NULL) // 偶数个元素
        {
            slow = slow->next_Node; // 走一步
            fast = fast->next_Node->next_Node; // 走两步
        }
        else // 奇数个元素的结尾
        {
            slow = slow->next_Node; // 奇数的中间
            fast = fast->next_Node;
        }
    }
    /* 0个或1个元素时 */
    if(slow->next_Node == NULL)
    {
        return false;
    }

    *e = slow->data;
    return true;
}