双向链表

当我们使用单链表时，会碰到取到某一结点后想访问其前驱节点的情况，这是只能再次遍历才能取到目标结点。这显然非常耗时间还不方便，由此就有了双向链表。

双向链表就是在原先单链表结点的基础上增加了一个指针域，用来存放其直接前驱结点的地址。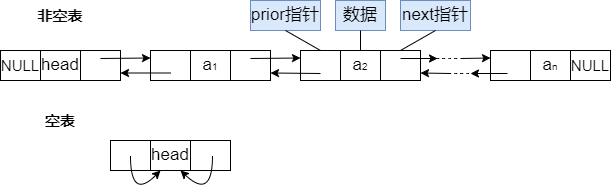

对于双向链表的操作可以说就是在单链表的基础上又多了一个对指针的操作。

相比于单链表，双向链表有效的提升了时间性能，也就是用空间换时间。

循环链表

对于单链表来说，每一个结点只有直接后继结点的地址，那么最后一个结点指向空；这就会导致不从头结点出发，就无法访问到所有结点。

为了解决上述问题，并可以循环访问链表，就有了循环链表。

其中单循环链表就是在单链表的基础上将终端结点的指针域从指向空变为指向头指针，这样使链表变成了一个环。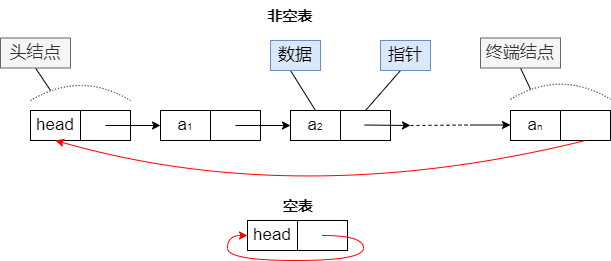

从上图可以看出，单循环链表和普通单链表并没有太大区别，就是将原先判断head->next_Node是否为NULL改为判断head->next_Node是否等于head。（由于单循环链表和单链表相似，这就不给出具体实现了）

有了这一特性，我们还可以再次升级设定：当不是空表时，增加一个指向终端结点的rear指针，此时就可以方便地访问该链表的头结点（rear->next_Node->next_Node）和最后一个结点（rear）了，时间复杂度都是O(1)，方便了连接两个链表等操作。

约瑟夫问题

据说著名犹太历史学家 Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式：41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。

然而Josephus和他的朋友想要活下去,于是Josephus假意遵从，将自己和朋友安排在第16和第31的位置，逃过了这场死亡游戏。

那么让我们用单循环链表来模拟死亡顺序：

#include <stdio.h>
#include <stdlib.h>
/* C语言要加这些，C++不用 */
#include <stdbool.h>
typedef struct Node Node;

typedef int Elem_Type;

struct Node // 结点
{
    Elem_Type data; // 数据域-人编号
    Node * next_Node; // 指针域
};
typedef struct Node Circular_Linked_List; // 方便区分代码中使用链表


void init_list(Circular_Linked_List **rear) // 将头指针改变指向头节点，因此参数是指针的指针
{
    Circular_Linked_List *head;
    Node *temp;
    /* 建立空表 */
    head = (Node *)malloc(sizeof(Node)); // 申请头节点空间
    head->data = 0;
    head->next_Node = head; // C++中可以把NULL全替换为nullptr
    /* 41个人 */
    temp = head;
    for(int i=1 ; i<=41 ; i++)
    {
        temp->next_Node = (Node *)malloc(sizeof(Node));
        temp = temp->next_Node;
        temp->data = i;
    }
    /*首尾相连*/
    *rear = temp;
    (*rear)->next_Node = head->next_Node;
    free(head); // 头结点可以去除,方便后续操作
}

void func()
{
    Circular_Linked_List *rear; // 演示rear指针
    Node *temp = NULL; // 遍历，报数人的前一个
    Node *delete_node = NULL; // 四大人
    int num = 0; // 人编号
    int all = 41; // 人数
    int count = 0; // 到3减一人
    init_list(&rear);
    temp = rear;
    while(all != 1)
    {
        count++;
        if(count == 3) // 到三则死
        {
            all--; // 人数减少
            count = 0;
            /* 死的人--删除结点 */
            delete_node = temp->next_Node;
            printf("%d->",delete_node->data);
            temp->next_Node = delete_node->next_Node;
            free(delete_node);
        }
        else // 遍历
        {
            temp = temp->next_Node;
        }
    }
    printf("%d",temp->data); // 最后一个人
}

int main()
{
    func();
    return 0;
}

相似的还有魔术师发牌问题：魔术师手中有A、2、3……J、Q、K十三张黑桃扑克牌。在表演魔术前，魔术师已经将他们按照一定的顺序叠放好（有花色的一面朝下）。魔术表演过程为：一开始，魔术师数1，然后把最上面的那张牌翻过来，是黑桃A；然后将其放到桌面上；第二次,魔术师数1、2；将第一张牌放到这些牌的最下面，将第二张牌翻转过来，正好是黑桃2；第三次，魔术师数1、2、3；将第1、2张牌依次放到这些牌的最下面，将第三张牌翻过来正好是黑桃3；……直到将所有的牌都翻出来为止。问原来牌的顺序是如何的。（结果：1 8 2 5 10 3 12 11 9 4 7 6 13）

循环链表还可以用于构建拉丁方阵（如下，一种n×n的方阵，方阵中恰有n种不同的元素，每种元素恰有n个，并且每种元素在一行和一列中恰好出现一次）。

判断是否有环

以下有两种简单方法来判断链表是否有环。

方法一

暴力双重循环：使用p，q两个指针，p一直往前走，q每次从头开始走，对于每一p到的结点，看两个指针的步数一不一样，不一样就说明有环。（在上图中，p走第六步到3时，q只用了三步，说明有环）

int has_loop1(Circular_Linked_List *head) // 可以返回环在第几个节点
{
    Node *q = head; // 一直前进
    int q_step = 0; // q步数
    while(q != NULL)
    {
        Node *p = head; // 从头开始
        int p_step = 0; // p步数
        while(p != NULL)
        {
            if(p == q)
            {
                /* 比较步数 */
                if(p_step == q_step)
                {
                    break;
                }
                else // 找到了
                {
                    return p_step+1;
                }
            }
            p = p->next_Node;
            p_step++;
        }
        q = q->next_Node;
        q_step++;
    }
    return 0;
}

方法二

快慢指针：使用fast和slow两个指针,slow每走一步，fast走两步，若存在fast == slow时说明环存在。（在上图中两指针会在4出相遇）

bool has_loop2(Circular_Linked_List *head)
{
    Node *fast = head;
    Node *slow = head;
    while(fast != NULL)
    {
        fast = fast->next_Node->next_Node;
        slow = slow->next_Node;
        if(slow == fast)
        {
            return true;
        }
    }
    return false;
}

双向循环链表

双向循环链表就是将上面两种链表相互结合。

双向循环空表和双向链表的空表一样。

实现

构建结点

typedef int Elem_Type;

typedef struct DCLNode// 结点
{
    Elem_Type data; // 数据域
    /* 指针域 */ 
    struct DCLNode *prior_Node; // 前一个
    struct DCLNode *next_Node; // 后一个
}DCLNode;
typedef DCLNode DCLinked_List; // 方便区分代码中使用链表
DCLinked_List *head;// 声明头指针*head

初始化

void init_list(DCLinked_List **head) // 将头指针改变指向头节点，因此参数是指针的指针
{
    *head = (DCLNode *)malloc(sizeof(DCLNode)); // 申请头节点空间
    (*head)->data = 0; // 头节点数据域初始化但不放数据
    (*head)->next_Node = *head; // 建立空表，C++中可以把NULL全替换为nullptr
    (*head)->prior_Node = *head;
}

清空

void clear_list(DCLinked_List *head)
{
    DCLNode *temp = NULL; // 临时存放要释放的下一个结点
    DCLNode *free_node = head->next_Node; // 存放要释放的结点
    /* 遍历清除 */
    while(free_node != head)
    {
        temp = free_node->next_Node; // 存放要释放的下一个结点
        free(free_node); // 释放结点
        free_node = temp; // 准备释放下一个节点
    }
    head->prior_Node = head;
    head->next_Node = head;
}

判空

bool list_is_empty(DCLinked_List head)
{
    if(head.next_Node == head.prior_Node) // 是否空表
    {
        return true;
    }
    return false;
}

获取表长

int list_length(DCLinked_List head)
{
    int count = 0; // 统计长度
    DCLNode *temp = head.next_Node; // 临时存放每一个结点
    /* 遍历计数 */
    while(temp->next_Node != head.next_Node)
    {
        count++;
        temp = temp->next_Node;
    }
    return count;
}

按值查找

查找，插入，删除都未采用循环计数

int list_locate_elem(DCLinked_List head,Elem_Type e)
{
    int count = 0; // 存放元素在表中的位置
    DCLNode *temp = head.next_Node; // 临时存放遍历结点
    /* 遍历定位 */
    while(temp->next_Node != head.next_Node)
    {
        count++;
        if(temp->data == e) // 找到元素
        {
            return count;
        }
        temp = temp->next_Node;
    }
    return 0;
}

按位查找并获取

bool list_get_elem(DCLinked_List head,int i,Elem_Type *e)
{
    DCLNode *temp = head.next_Node; // 临时存放遍历结点
    int count = 1; //  计数，到i时停止查找
    /* 定位遍历 */
    while(temp->next_Node!=head.next_Node && count<i )
    {
        temp = temp->next_Node;
        count++;
    }
    /* 定位失败 */
    if(temp->next_Node==head.next_Node || count>i) // 没找到元素或传入的i<1
    {
        return false;
    }

    *e = temp->data;
    return true;
}

由于双向循环链表多了一个指针域且循环，因此插入和删除要格外小心

插入

bool list_insert(DCLinked_List *head,int i,Elem_Type e)
{
    DCLNode *temp = head->next_Node; // 找出要插入的后一个结点
    DCLNode *insert_node = NULL; // 要插入的结点
    int count = 1; // 计数
    /* 遍历到要插入的前一个结点 */
    while(count<i && temp!=head)
    {
        temp = temp->next_Node;
        count++;
    }
    /* 插入失败 */
    if(count>i || temp==head) // i<1或i超出可插入范围（i>表长+1）
    {
        return false;
    }

    insert_node = (DCLNode *)malloc(sizeof(DCLNode)); // 申请插入的结点空间
    insert_node->data = e;
    /* 插入 */
    insert_node->next_Node = temp;
    temp->prior_Node->next_Node = insert_node;
    insert_node->prior_Node = temp->prior_Node;
    temp->prior_Node = insert_node; // 必须在最后
    return true;
}

删除

bool list_delete(DCLinked_List *head,int i,Elem_Type *e)
{
    // DCLNode *temp = NULL; // 存放要删除的前一个结点
    DCLNode *deleted_node = head->next_Node; // 要删除的结点
    int count = 1;
    /* 找出要删除的前一个结点 */
    while(deleted_node!=head && count<i)
    {
        deleted_node = deleted_node->next_Node;
        count++;
    }
    /* 删除失败 */
    if(count>i || deleted_node==head) // i<1或i超出可插入范围（i>表长+1）
    {
        return false;
    }
    /*删除*/
    *e = deleted_node->data;
    deleted_node->prior_Node->next_Node = deleted_node->next_Node;
    deleted_node->next_Node->prior_Node = deleted_node->prior_Node;
    return true;
}

头插法

void list_push_front(DCLinked_List *head,Elem_Type e)
{
    DCLNode *temp = (DCLNode *)malloc(sizeof(DCLNode)); // 要插入的结点
    temp->data = e;
    /* 插入 */
    temp->next_Node = head->next_Node;
    head->next_Node->prior_Node = temp;
    temp->prior_Node = head;
    head->next_Node = temp;
}

尾插法

void list_push_back(DCLinked_List *head,Elem_Type e)
{
    DCLNode *temp = (DCLNode *)malloc(sizeof(DCLNode)); // 最后的结点
    temp->data = e;
    temp->prior_Node = head->prior_Node;
    head->prior_Node->next_Node = temp;
    temp->next_Node = head;
    head->prior_Node = temp;
}

其他部分

void create_10elem_list(DCLinked_List *head)
{
    for(int i=1 ; i<=10 ; i++)
    {
        list_push_back(head,i); // 尾插法插入10个元素
    }
}

void print_list(DCLinked_List head)
{
    DCLNode *temp = head.next_Node;
    while(temp->next_Node != head.next_Node)
    {
        if(sizeof(Elem_Type) == 4)
        {
            printf("%d ",temp->data);
        }
        temp = temp->next_Node;
    }
    printf("\n");
}

bool get_mid_elem(DCLinked_List *head,Elem_Type *e)
{
    DCLNode *fast = head; // 快指针
    DCLNode *slow = head; // 慢指针
    while(fast->next_Node != head)
    {
        if(fast->next_Node->next_Node != head) // 偶数个元素
        {
            slow = slow->next_Node; // 走一步
            fast = fast->next_Node->next_Node; // 走两步
        }
        else // 奇数个元素的结尾
        {
            slow = slow->next_Node; // 奇数的中间
            fast = fast->next_Node;
        }
    }
    /* 0个或1个元素时 */
    if(slow->next_Node == head)
    {
        return false;
    }

    *e = slow->data;
    return true;
}